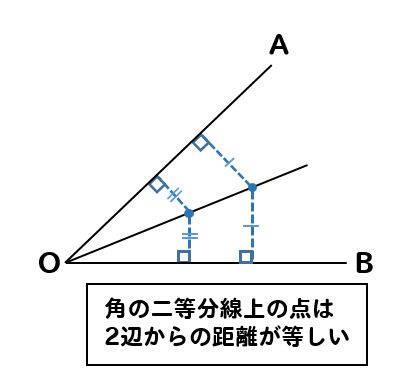
角の二等分線とは? 定理や比の性質、証明、問題、作図方法 21年2月19日 この記事では、「角の二等分線」の定理や性質をついてわかりやすく解説をしていきます。 また、定理の証明や作図方法、問題の解き方も紹介していくので、ぜひこの記事を通し トップ 100 台形 の 書き方 小 4 コンパス 5年算数 図形の角と合同 5 合同な四角形をかこう Youtube 台形 平行四辺形 Youtube 小4 図形の書き方 ママの交流掲示板 ママスタ s 三角定規で台形を作る おときち副塾長 電脳空間学習塾かもん Youtube 5年算数 図形の角角の二等分線は、 2 2 つの直線から等距離にある点の集合です。 単純に、「 2 2 辺からの距離が等しい直線は角の二等分線」ともいいます。 垂直二等分線の作図と角の二等分線の作図。 必ず暗記しましょう。 これがすべての作図に通ずる超重要事項です

見えない角の二等分線のやり方 見えない角の二等分線とは 普通の角の 中学校 教えて Goo
三角形 二等分線 書き方
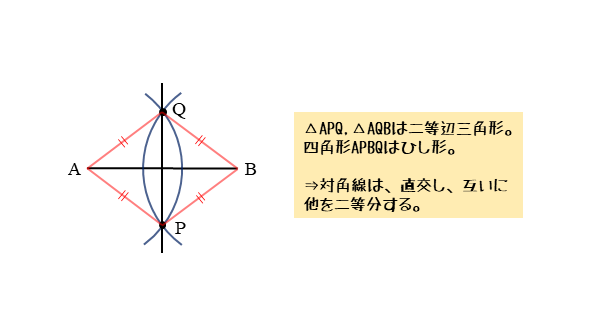
三角形 二等分線 書き方-外接円、外心について 「外接円」や「外心」の用語や意味は中学の 教科書の発展内容としてあります。 それぞれの各辺の垂直二等分線は一点でまじわり、その点Dを中心に円を書くと Dを中心に三角形の3つの頂点を通る円を書くことができて、この円以上が垂直二等分線の書き方ですが、「なぜこれが垂直二等分線になるのか」についても解説していきます。 垂直二等分線になる理由 まず、ふたつの弧が交わる点について考えてみましょう。 これらはどういった点なのでしょうか?




中1数学 垂直二等分線の作図 練習編 映像授業のtry It トライイット
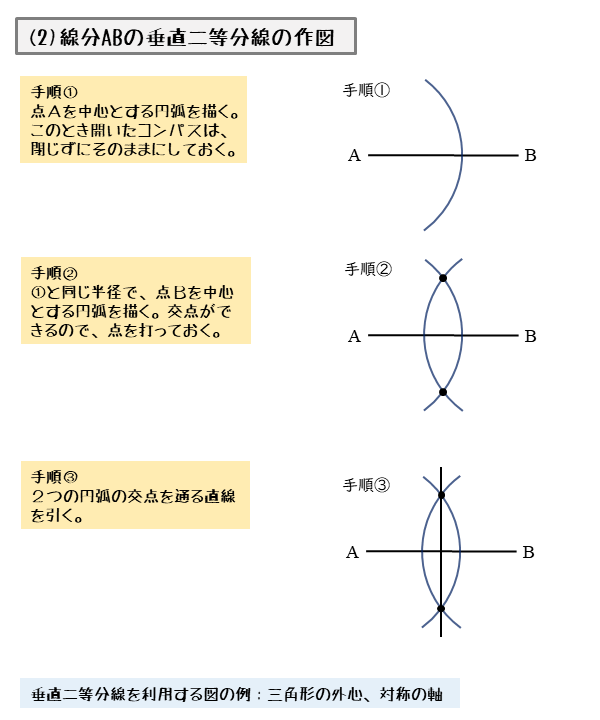
正三角形の中点を結ぶ。 中点は線分の垂直二等分線により見つける。それを2枚並べる。(図5) ウ. 正六角形の一つの角1°を30°+90°に分けてつくる。まず,30°の角をつくり,次に長方形をつくるAB=a, AC=b, BD=d, AB = a,AC = b,BD = d, DC=e, AD=f DC = e,AD = f とおくとき以下の公式が成立する。 1:ae=bd 1:ae = bd 2: (ab)f=2ab\cos \dfrac {A} {2} 2:(a b)f = 2abcos 2A こんにちは、ウチダです。 今日は、中学1年生で習う 「垂直二等分線」 について、その作図方法とそれが正しいことの証明を解説したのち、実際に作図問題で練習し、最後に垂線の作図も考察していきます。 垂直二等分線の書き方 垂直二等分線とは、読んで字のごとく「垂直」で線分を「二
三角形の頂点とその 対辺の中点 を通る直線は三角形の面積を二等分する。 頂点bを通る直線が辺acの中点を通れば abcの面積を二等分することになる。 中点 a(3, 12), c(13, 2)よりacの中点は(8, 7)である。つ\ある操作" を加えて三等分する方法をお話します。特に、 角の三等分は古代からの数学上の未解決問題の一つでした。 本講座では、実際に、定規とコンパスを使って作図してみま す。定規とコンパスをご準備ください。 1.二等分 2.古代の三大作図問題角度を単位円上の点として扱う幾何代数の技法によって、角の二等分線の性質を確認します。 クリフォード代数は使用しないで、複素平面上でオイラーの公式に基づく計算を行います。 ※ 図は Markdown に SVG を直接記述しています
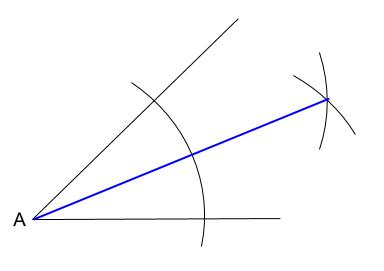
正三角形の作図を利用する 2.30°の作図は、 60°の角の二等分線を 利用する 3.90°の作図は、 垂線を利用する 4.45°の作図は、 90°の角の二等分線を 利用する 5.1°の作図は、 60°の角の作図 (180°-60°)を 利用する 6.その他の 角の二等分線の書き方手順 まずは二等分したい角がある頂点にコンパスの針をおき、2辺と交わるように円をかきます。 次に、先ほどの円と2辺が交わった点にコンパスの針をおき、 同じ大きさの円を2つかきます。垂直二等分線の方程式の求め方を2通り解説 中点連結定理とその逆の証明および例題 角の二等分線定理(内角、外角それぞれ) 二等辺三角形の底角が等しいことの証明など 鋭角三角形と鈍角三角形の意味と見分け方 三角形の合同条件を図で分かりやすく説明
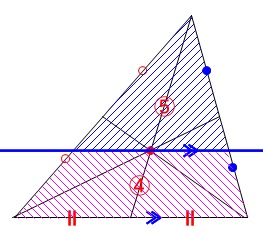



三角形の面積を直線が二等分する2つのパターン




角の二等分線と比の定理とは 作図方法 書き方 や性質の証明を解説 外角の問題アリ 遊ぶ数学
やり方は ①円O上に適当な点を取る (B) ②点Bと中心Oを通る直線を引く ③ABの垂直二等分線をかきBOと 円に外接、内接する多角形の書き方です。 どちらも、多角形コマンドで書けます。 操作方法 ・内接する多角形 多角形 ー中心→頂点指定を選択 ーとし,BCとの交点をPとすると PB:PC=AB:AC である. 証明 頂点B,頂点Cから二等分線 ℓ 角の二等分線と垂線 – GeoGebra Materials まず、 AB = c 、 AC = b 、 AD = d とし、 AD は ∠ BAC の2等分線なので、補題より、 BD = a c b c 、 DC = a b b c です。 ここで A から辺 BC に垂線を下ろし、交点を E とします。 直角三角形 ABE について c 2 = A E 2 B



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典



中1 作図 3辺から等しい距離にある点の作図方法とは 数スタ
三角形の五心⑤ 三角形の傍心とその存在証明 スポンサーリンク 高校数学A 平面図形 検索用コード 三角形の1つの内角の二等分線と他の頂点の外角の二等分線は1点で交わる}}} \\ 2zh その交点を傍心は {1辺と他の2辺の延長からの距離が等しい点方法4の辺の取り方の変更です。 方法8 二等分線とABの交点Dが、3等分点のひとつになります。 (説明) ABC、 CBDはともに、30°を含む直角三角形です。 3等分点になっています。 方法9 二等分線の長さ 三角形の角の二等分線の長さ 今回の公式はコチラ 一見、こんな計算で三角形の角の二等分線の長さを求めることができるのか不安ですが、ちゃんと求めることができます。 では、この公式の証明をしていきましょう。 証明 下ごしらえ
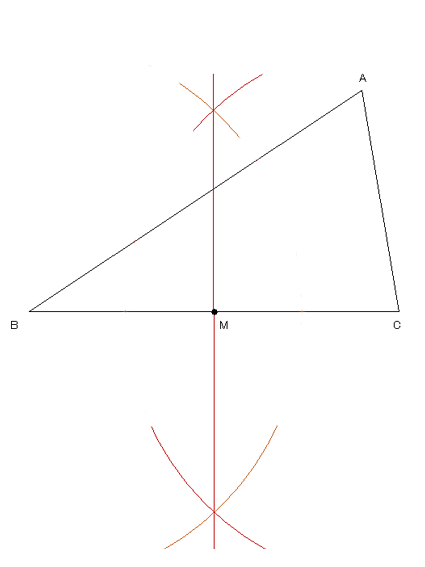



平面図形 練習問題 14 ネット塾




垂直二等分線の作図方法 書き方 と なぜ正しいのか 証明をわかりやすく解説 垂線 遊ぶ数学
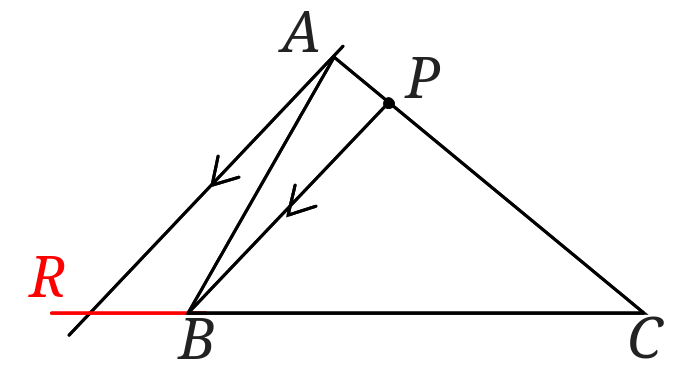
二次関数のグラフで三角形の面積を求める問題の解き方の4ステップ 中1数学 中学1年数学文字式を勉強すると便利な2つの理由 中1数学 2分でわかる!扇形(おうぎ形)の弧の長さの求め方 中2数学 入試前の復習にピッタリ! 等積変形を使って二等分線を書く 右のような三角形があります。 点\(P\)を通る\(\triangle ABC\)の面積を二等分する直線を書きましょう。 この問題は、二次関数のなかで三角形の面積を二等分するときに使うことができます。(1) 基本となる直線を描く。 (2) 直角三角形の長い辺を(1)の直線に合わせる。 (3) 二等辺三角形の直角のある辺を(2)の直角三角形の長い辺にあてて、垂直線を引きたい位置に合わせる。
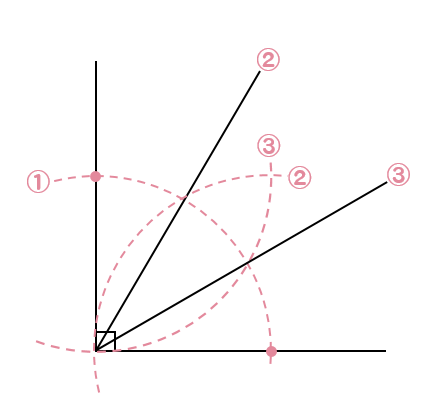



中1作図 直角90度を三等分する線の書き方を解説 数スタ
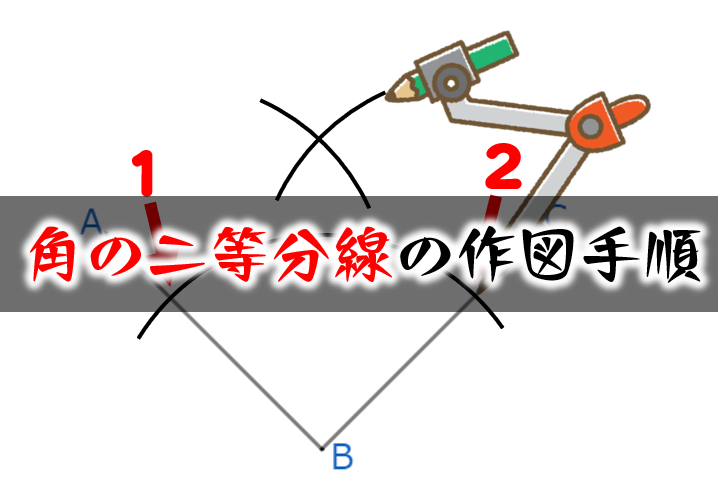



角の二等分線 の作図方法 コンパス 定規 数学fun
(4) 正三角形の完成。 直線定規を使った正三角形の描き方 定規の目盛りで直線の長さを測る。 ☆用具:直線定規(直角を描くための三角定規または分度器) (1) 底辺となる直線abを描き、垂直二等分線を引く。 (2) 点aから垂直二等分線まで、底辺と同じ長さ三角形の内接円・外接円の書き方を解説! 直角を三等分する線の作図方法とは 回転移動の中心を求める方法とは?作図の方法を解説! 最短距離にするためにはどこを通る?? 平行四辺形の書き方、コンパスを使って作図する方法は?放物線と三角形の面積 (中学3年の放物線と直線の交点も使う) == 三角形の面積の二等分線 == 三角形の面積は (面積)=(底辺)×(高さ)÷2 の公式で求められます. 次の図のように, ABC の頂点 A から対辺 BC の中点(真ん中の点,1対1に内分する点
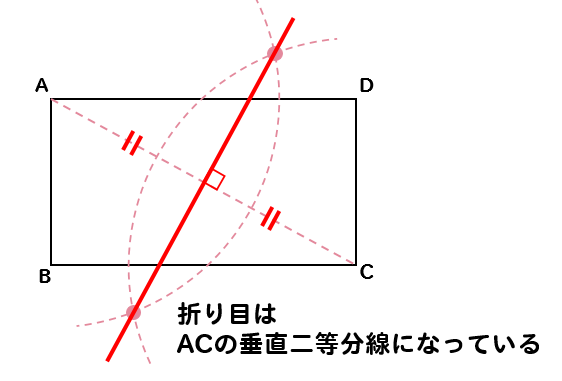



作図 垂直二等分線のやり方は どんな問題で使えるのか解説 数スタ




基本の作図 4ステップでわかる 垂直二等分線の書き方 Qikeru 学びを楽しくわかりやすく
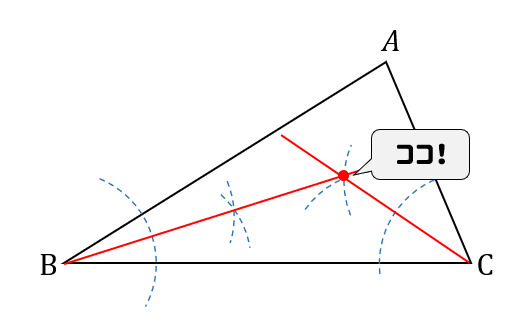
三角形の内心 ・ 外心 ・ 重心 三角形の3つの内角の2等分線は、1点で交わり、その点から3辺までの距離は等しい。 この1点で交わった点 I を三角形の内心という。 半径 IL の円が三角形の内接円である。




中1数学 垂直二等分線の作図 練習編 映像授業のtry It トライイット




この問題はの答えは 角bの角の二等分線を使って点pを作図するのですが 線分 Ac Clear




面積を二等分する直線 Youtube




基本の作図 4ステップでわかる 垂直二等分線の書き方 Qikeru 学びを楽しくわかりやすく



Abcの頂点aを通り 面積を2等分する直線の書き方を教えてく Yahoo 知恵袋




角の三等分線の一般的な作図法はないということをあやふやに説明する もりぶろ
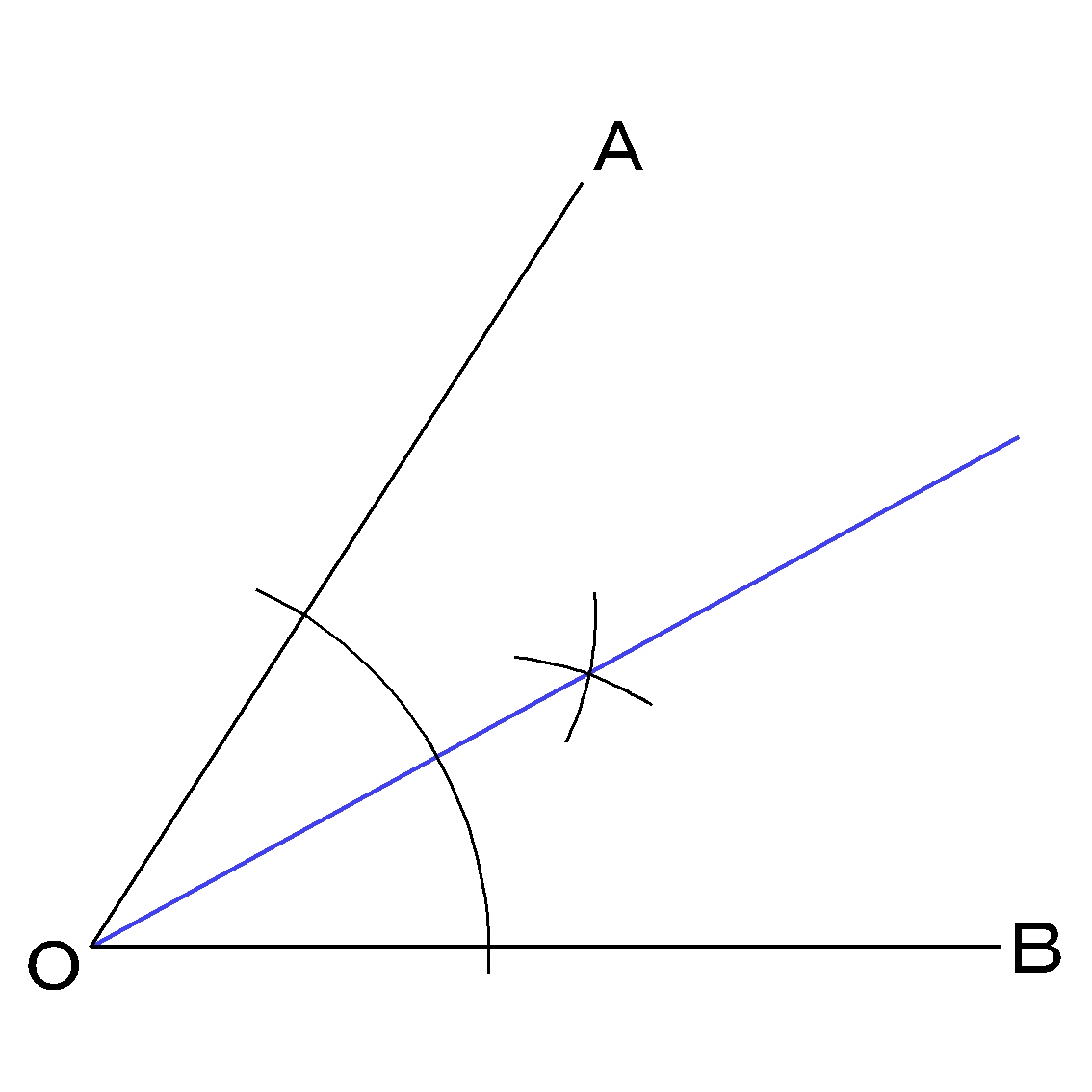



角の二等分線 Wordで数学問題プリントを作ろう
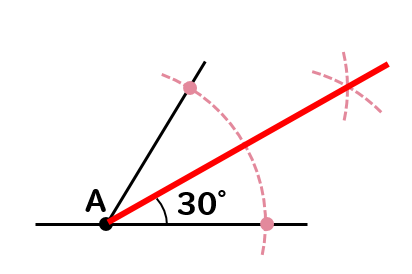



作図 角の二等分線のやり方は どんな問題で使えるのか解説 数スタ




作図 線分の3等分 中学数学の無料オンライン学習サイトchu Su
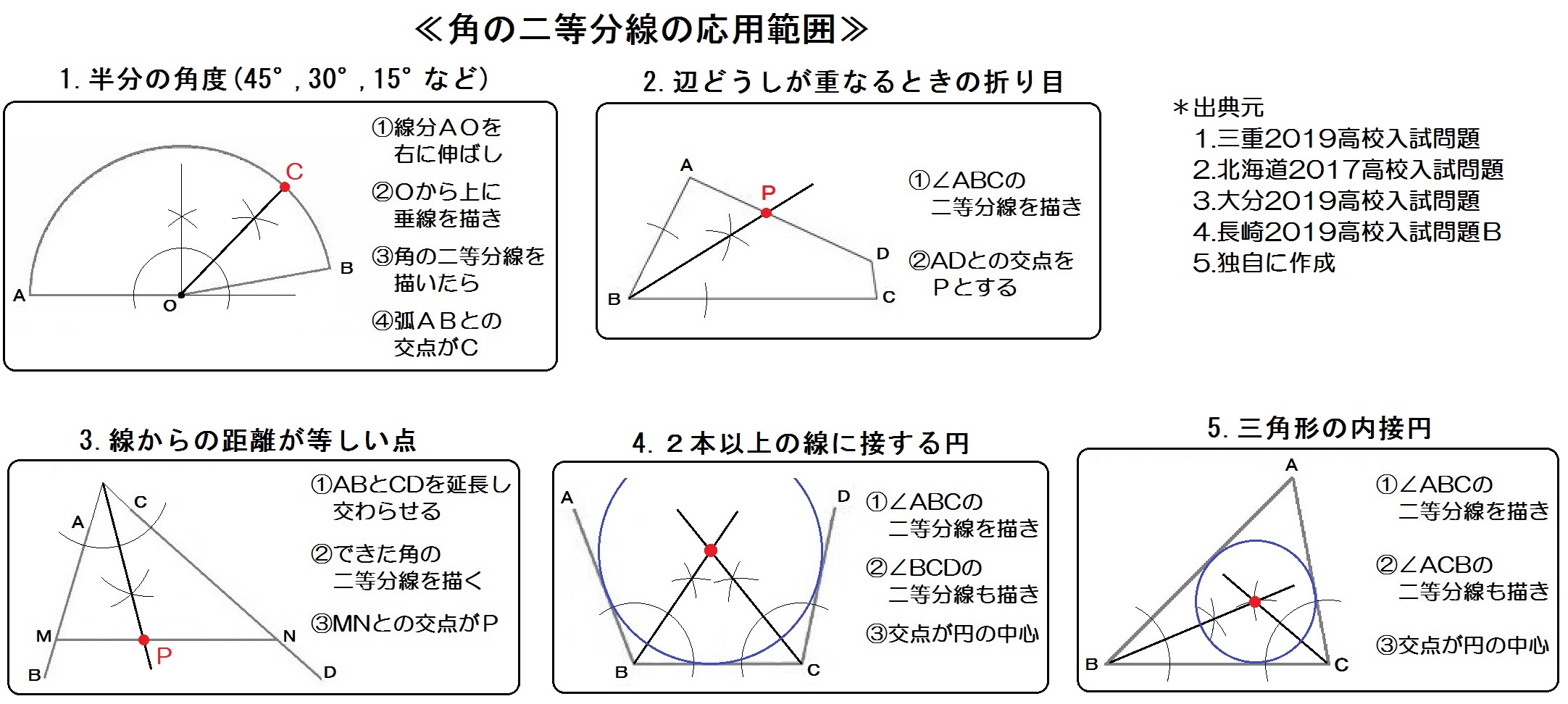



中学数学 平面図形 のコツ 角の二等分線 垂線を使った作図




角の二等分線の作図 手順と なぜ について解説します 中学数学 理科の学習まとめサイト
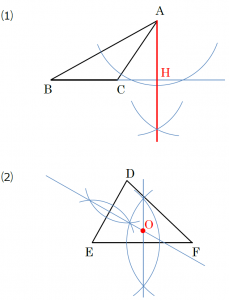



中1数学 垂直な線の作図のしかた まなビタミン
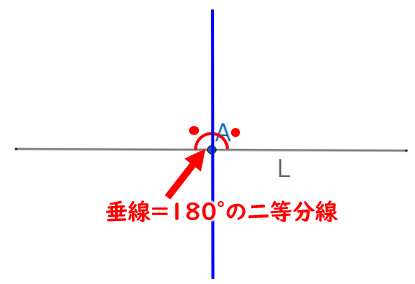



角の二等分線 の作図方法 コンパス 定規 数学fun



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典




基本の作図 5ステップでわかる 角の二等分線の書き方 Qikeru 学びを楽しくわかりやすく
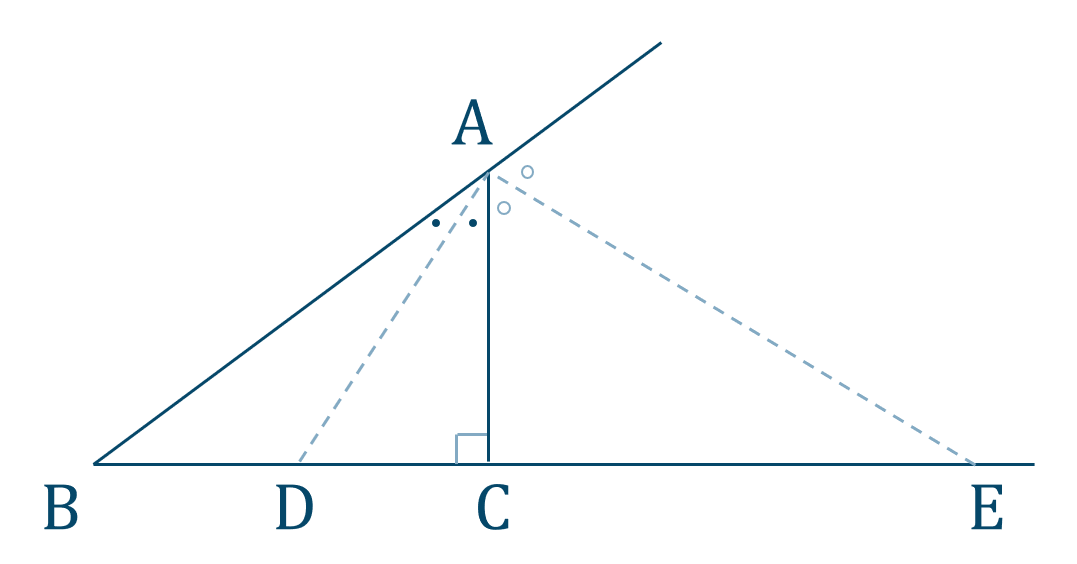



数学a 角の二等分線と比の使い方とコツ 教科書より詳しい高校数学
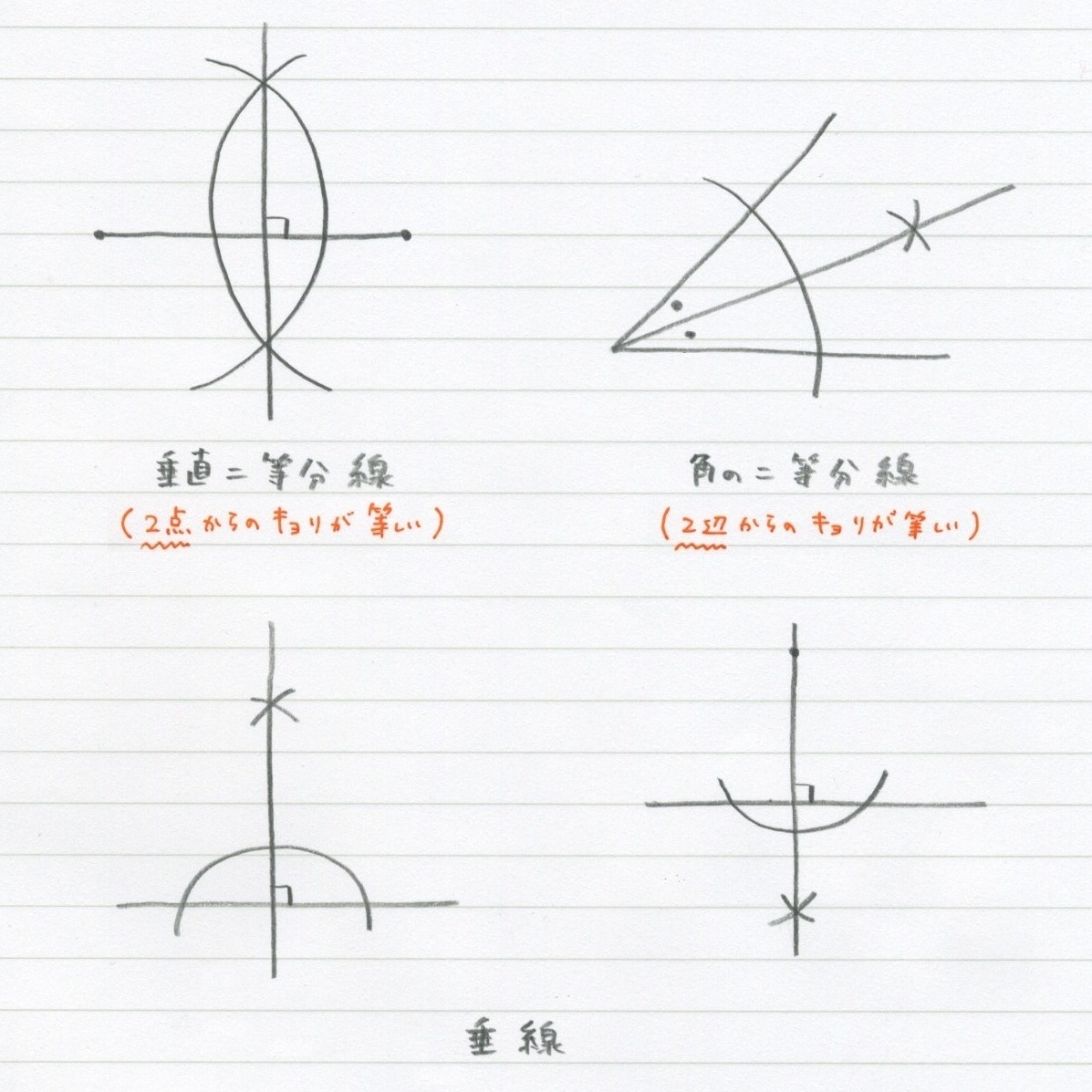



12 1 作図 結局4つ 勉強できようサイト
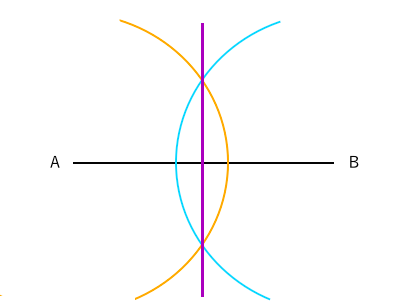



垂直二等分線を作図する 目 を描く 苦手な数学を簡単に




角の二等分線と比の定理とは 作図方法 書き方 や性質の証明を解説 外角の問題アリ 遊ぶ数学



1



角の二等分線をひく 中学から数学だいすき
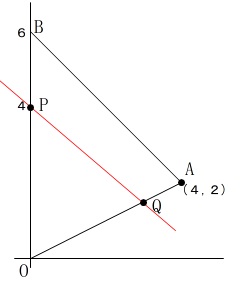



三角形の面積を直線が二等分する2つのパターン
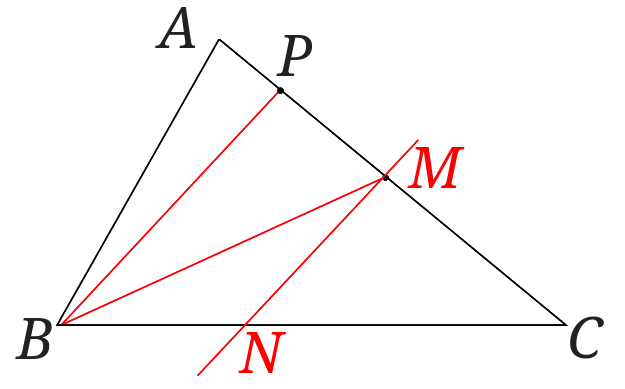



等積変形の作図で四角形を三角形にする作図や二等分線の引き方 まぜこぜ情報局



図形の性質 作図について 日々是鍛錬 ひびこれたんれん
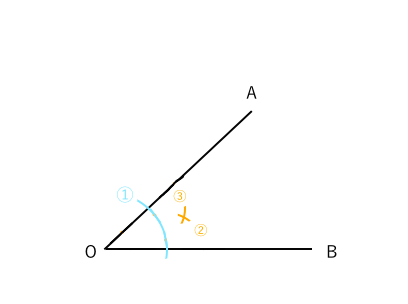



簡単にわかる 角の二等分線を作図する方法 苦手な数学を簡単に




角の二等分線の作図 Youtube




角の二等分線 の作図方法 コンパス 定規 数学fun



三角形の3つの辺の垂直二等分線の作図の仕方を教えてください 急ぎ Yahoo 知恵袋



図形の性質 作図について 日々是鍛錬 ひびこれたんれん




角の二等分線の作図 手順と なぜ について解説します 中学数学 理科の学習まとめサイト




角の二等分線と比の定理とは 作図方法 書き方 や性質の証明を解説 外角の問題アリ 遊ぶ数学
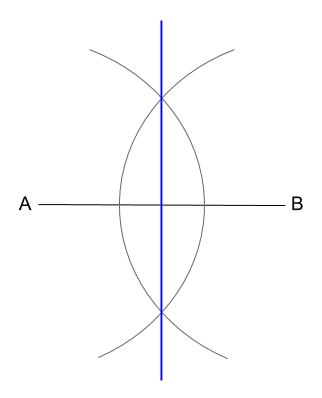



中学数学 作図 垂直二等分線 角の二等分線 中学数学の無料オンライン学習サイトchu Su



等積変形の作図で四角形を三角形にする作図や二等分線の引き方 まぜこぜ情報局



中学数学 作図 垂直二等分線 角の二等分線 中学数学の無料オンライン学習サイトchu Su




内心とは 三角形の内心の求め方や比の使い方 性質の証明 位置ベクトルをわかりやすく解説 遊ぶ数学




作図ー角の二等分線 無料で使える中学学習プリント



三角形に接する円 中学から数学だいすき




基本 垂線二等分線の作図 なかけんの数学ノート



作図 角の二等分線のやり方は どんな問題で使えるのか解説 数スタ
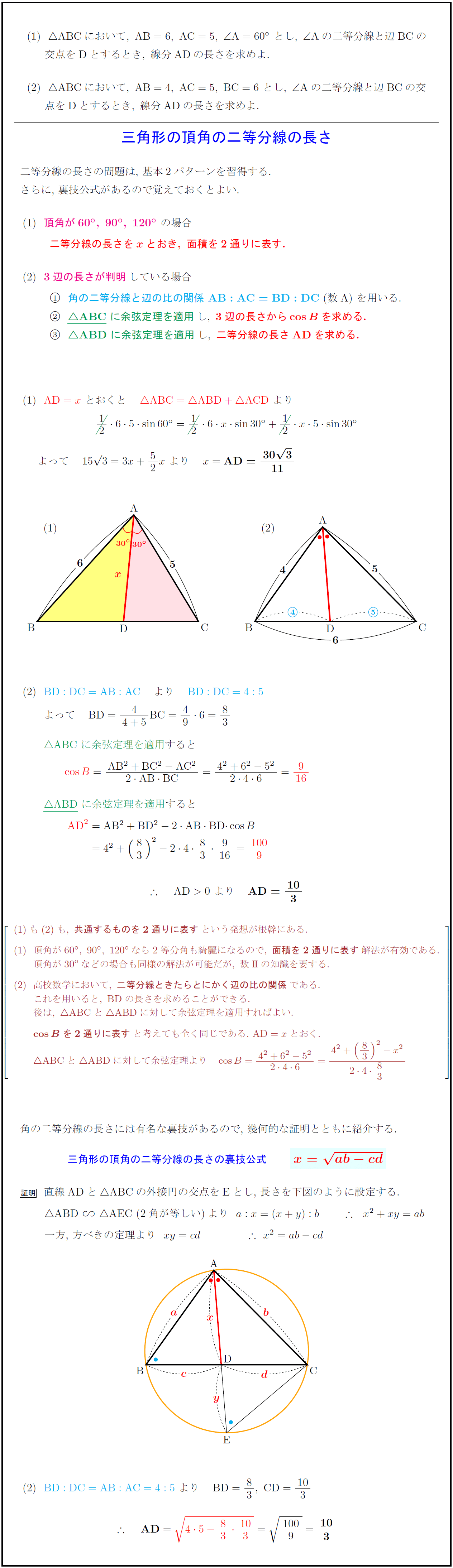



高校数学 三角形の頂角の二等分線の長さ 基本2パターン 裏技公式 X Ab Cd とその証明 受験の月



コラム
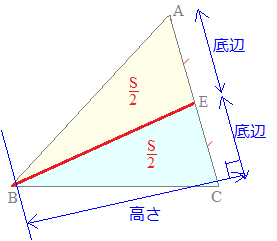



三角形の面積の二等分線
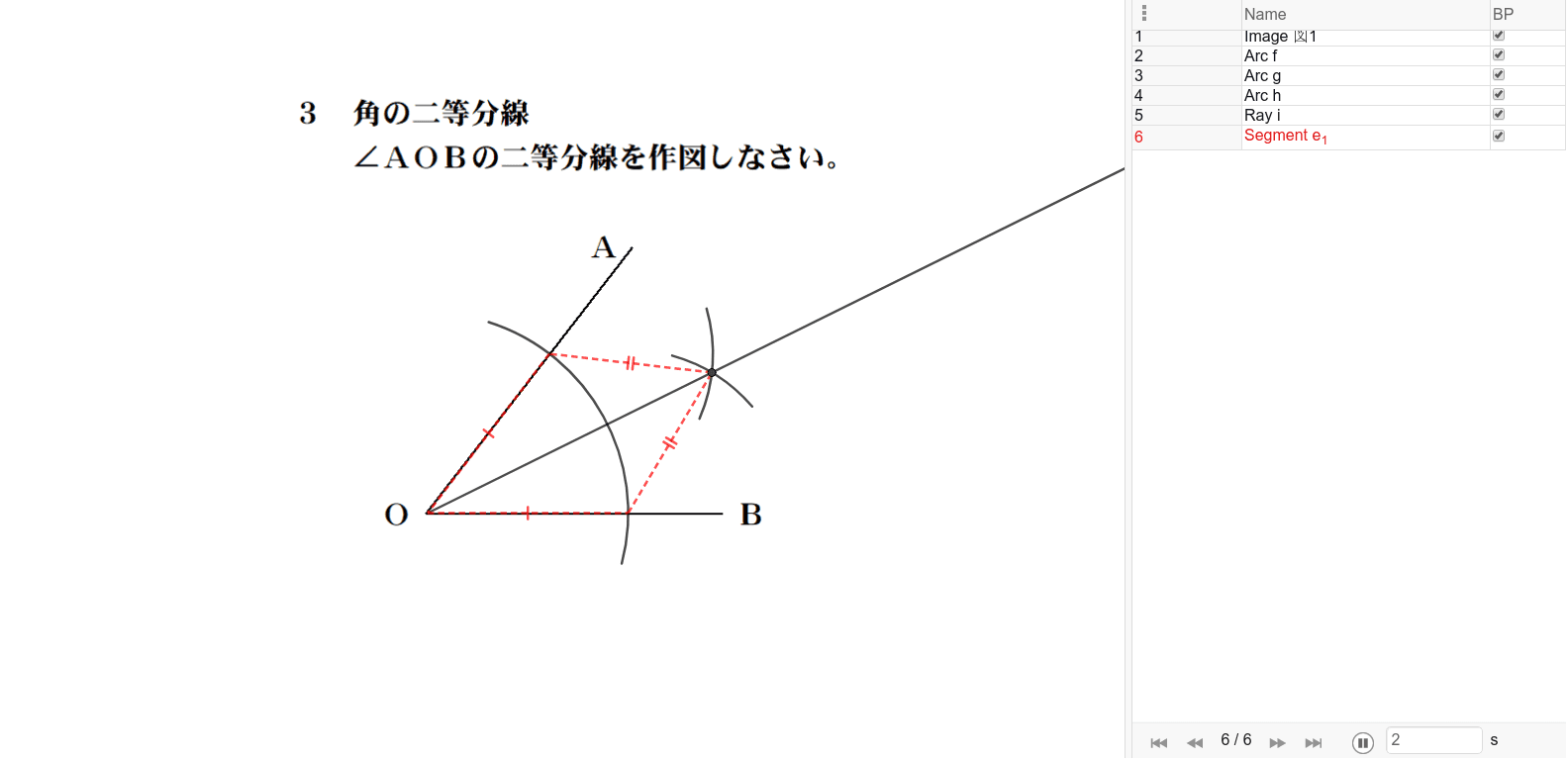



角の二等分線の作図 Geogebra



三角形の面積の二等分線




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




見えない角の二等分線のやり方 見えない角の二等分線とは 普通の角の 中学校 教えて Goo



三角形の面積を二等分する 垂線 理系男子の独り善がり



外接円 外心について




角の二等分線と比の定理とは 作図方法 書き方 や性質の証明を解説 外角の問題アリ 遊ぶ数学



中3数学 角の二等分線定理のポイントと練習問題




等積変形とは 台形から三角形に変える問題を解説 応用問題 難問アリ 遊ぶ数学



Q Tbn And9gcrbpajgfjly5hfkvvdnnyu23ye9ydzs7n1fi7sas6ubptrfplj6 Usqp Cau




基本 角の二等分線の作図 なかけんの数学ノート




中1 数学 平面図形7 垂直二等分線の作図 8分 Youtube




基本の作図 5ステップでわかる 角の二等分線の書き方 Qikeru 学びを楽しくわかりやすく




弦の垂直二等分線上に円の中心は本当にあるのか 数学が嫌いなんです



内接円 内心
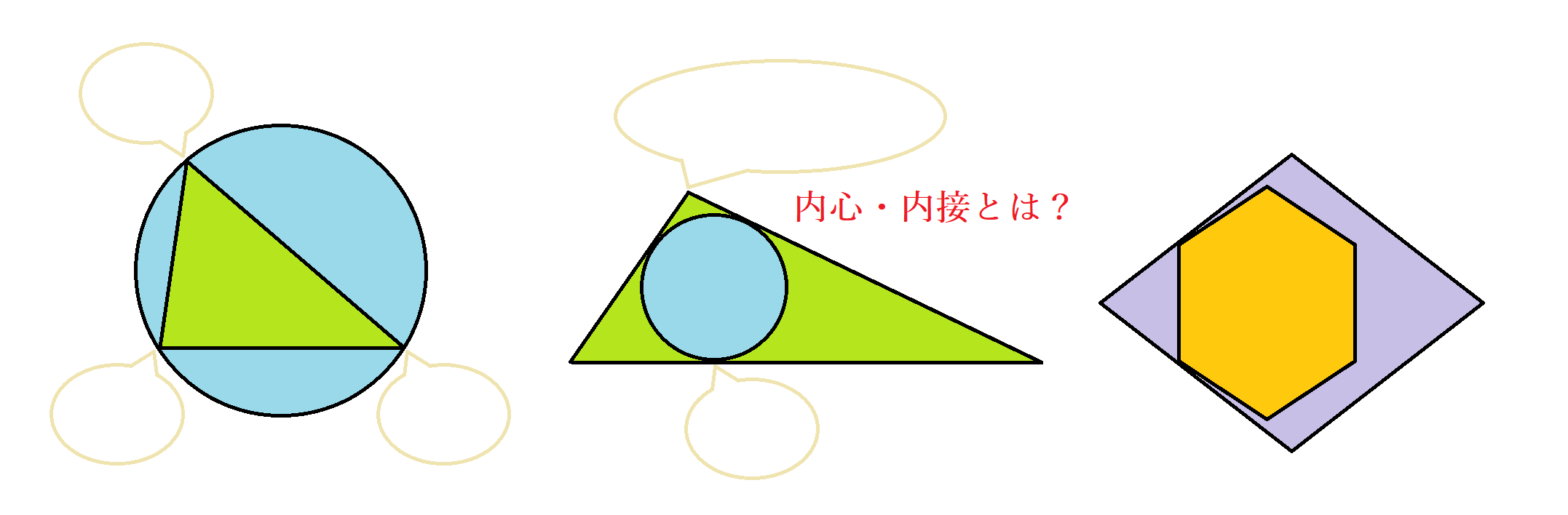



数学 三角形の内心とは 角の二等分線の作図を踏まえた内接円の書き方と証明 Curlpingの幸せblog
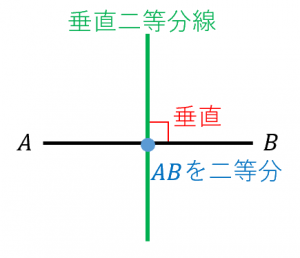



垂直二等分線の意味と作図方法を分かりやすく解説 具体例で学ぶ数学



コンパスと定規を使った垂直線の描き方 図形の描き方001a 夏貸文庫
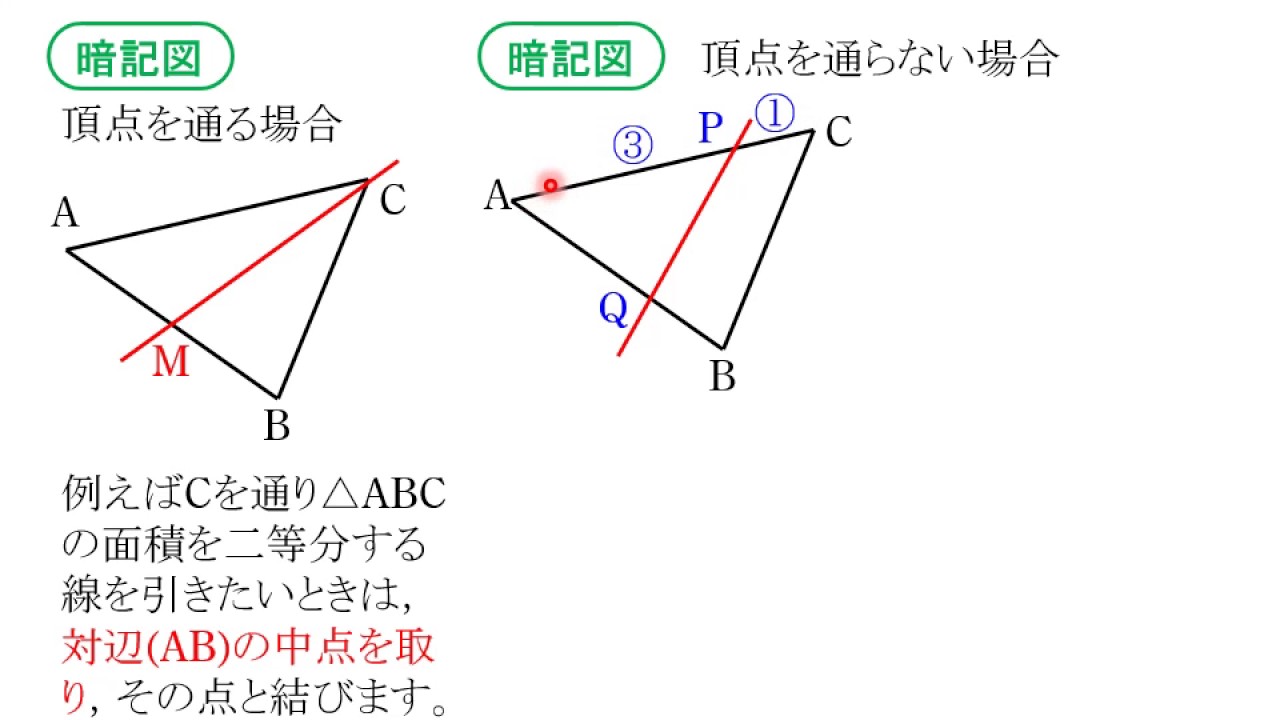



関数12 三角形の面積の二等分 Youtube
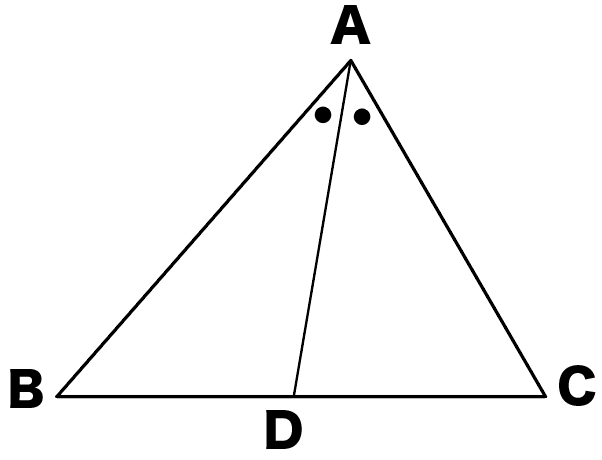



三角形の角の二等分線の性質 定理の証明がわかる5ステップ Qikeru 学びを楽しくわかりやすく




垂直二等分線 の作図方法 コンパス 定規 数学fun



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典




基本の作図 5ステップでわかる 角の二等分線の書き方 Qikeru 学びを楽しくわかりやすく



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典




高校数学a 角の二等分線と比の利用 練習編 映像授業のtry It トライイット



1
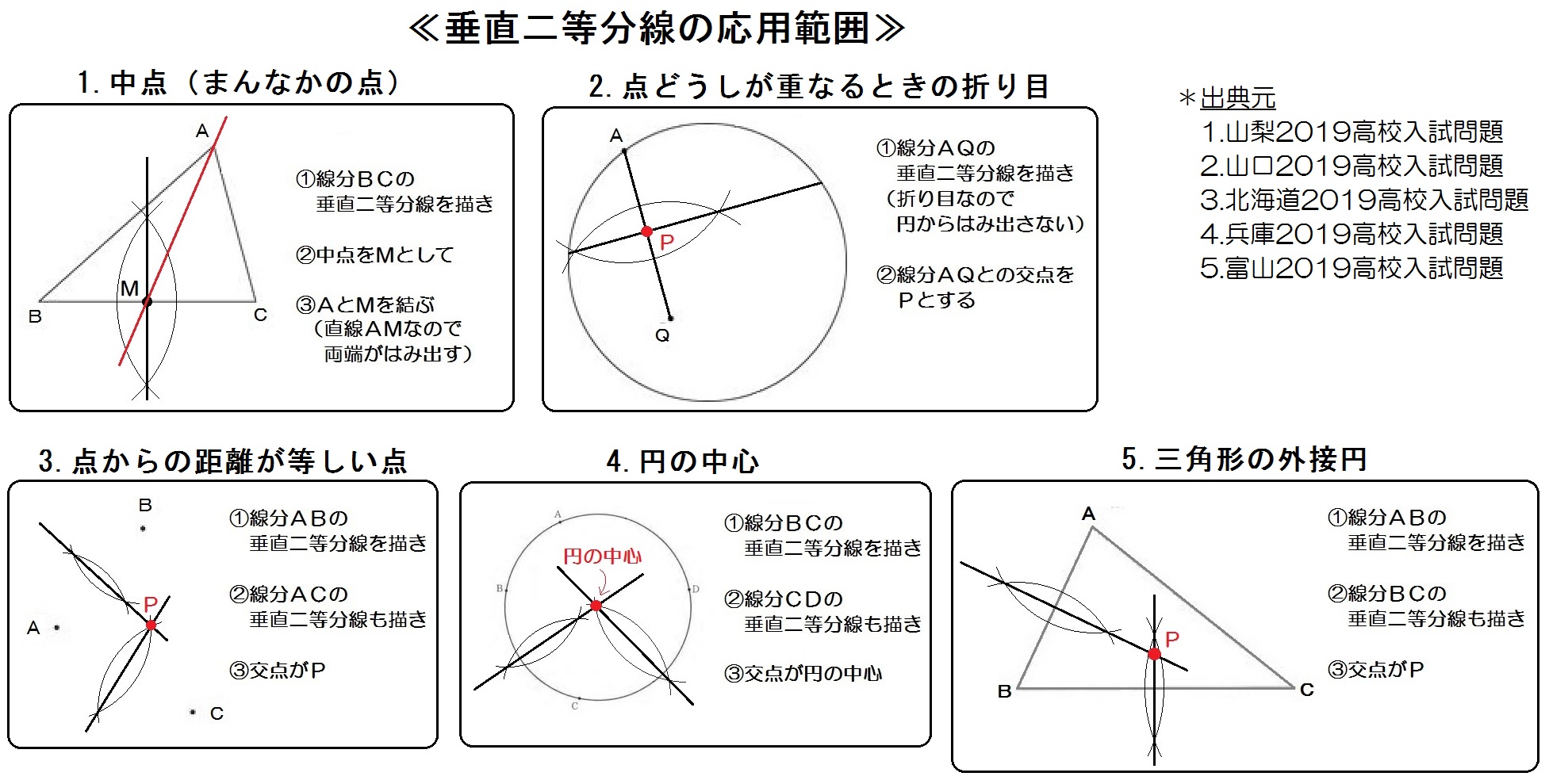



中学数学 平面図形 のコツ 角の二等分線 垂線を使った作図



1




角の二等分線と比の定理とは 作図方法 書き方 や性質の証明を解説 外角の問題アリ 遊ぶ数学




中1数学 垂直二等分線の作図 練習編 映像授業のtry It トライイット




角の二等分線の作図 手順と なぜ について解説します 中学数学 理科の学習まとめサイト
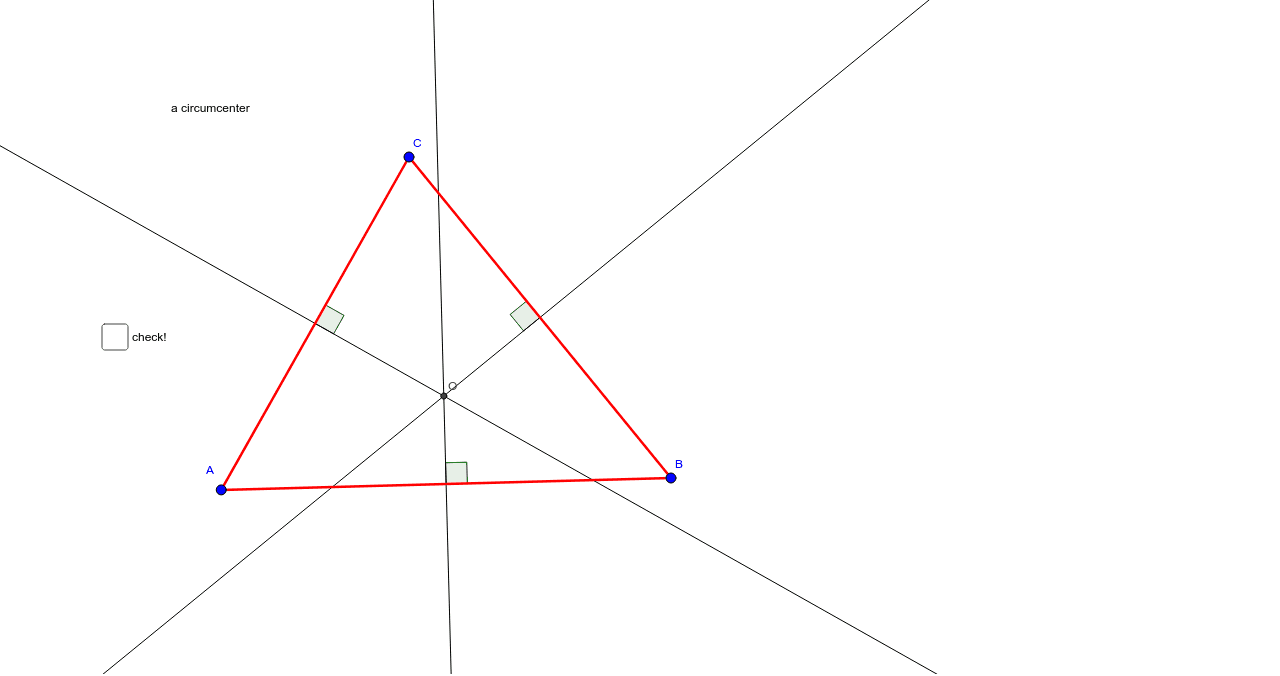



三角形の辺の垂直二等分線 A Circumcenter Geogebra
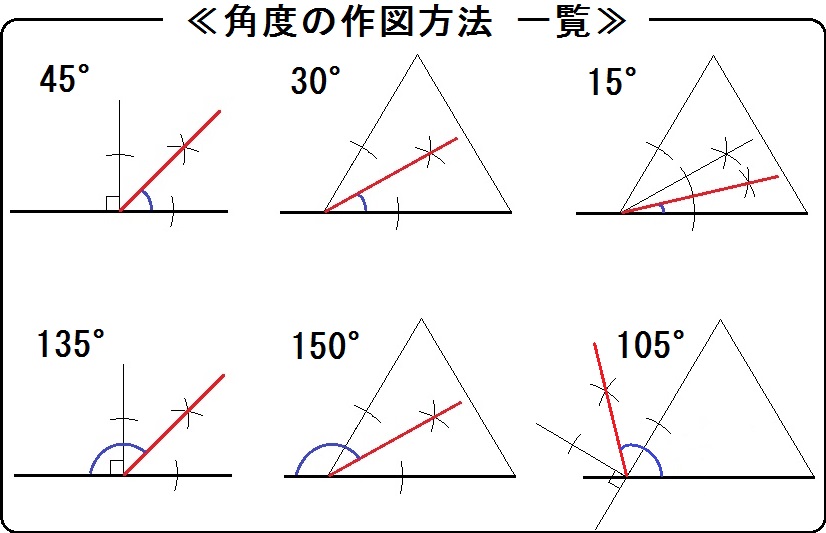



中学数学 平面図形 のコツ 角の二等分線 垂線を使った作図




標準 垂線や二等分線の作図 なかけんの数学ノート
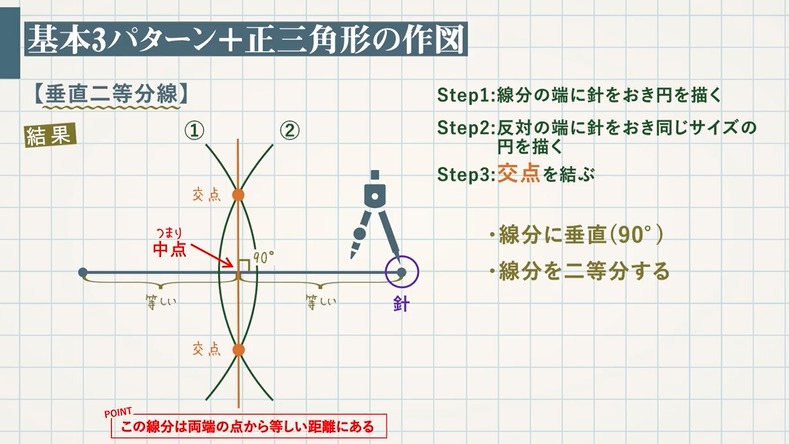



1年生で習う作図まとめ 教遊者
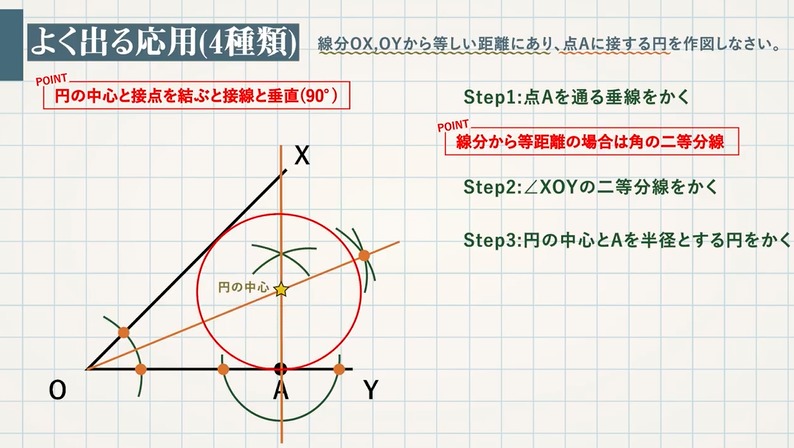



1年生で習う作図まとめ 教遊者
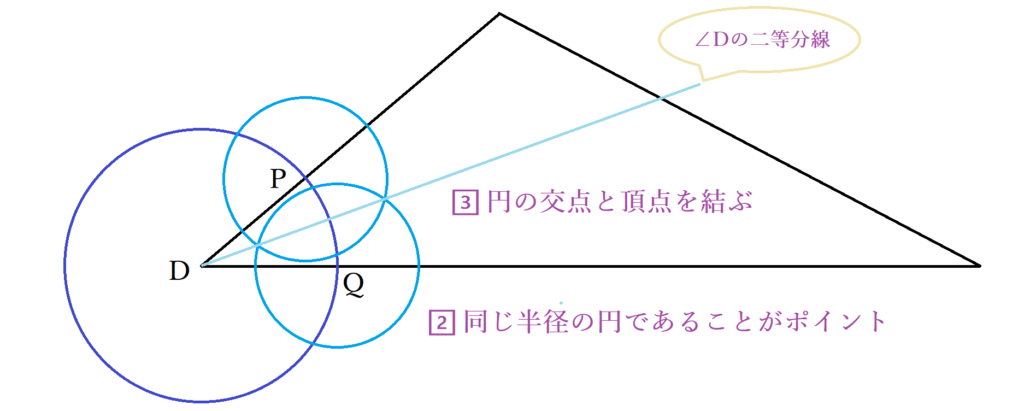



数学 三角形の内心とは 角の二等分線の作図を踏まえた内接円の書き方と証明 Curlpingの幸せblog
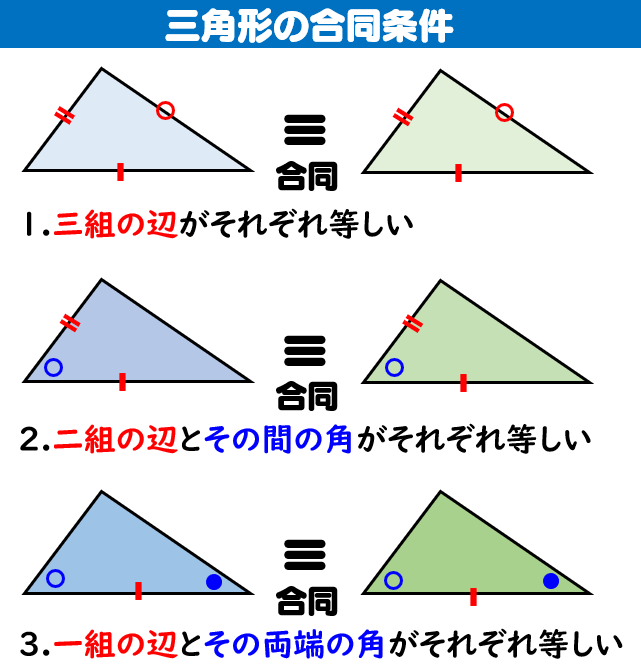



角の二等分線 の作図方法 コンパス 定規 数学fun




見えない角の二等分線のやり方 見えない角の二等分線とは 普通の角の 中学校 教えて Goo




基本の作図 5ステップでわかる 角の二等分線の書き方 Qikeru 学びを楽しくわかりやすく
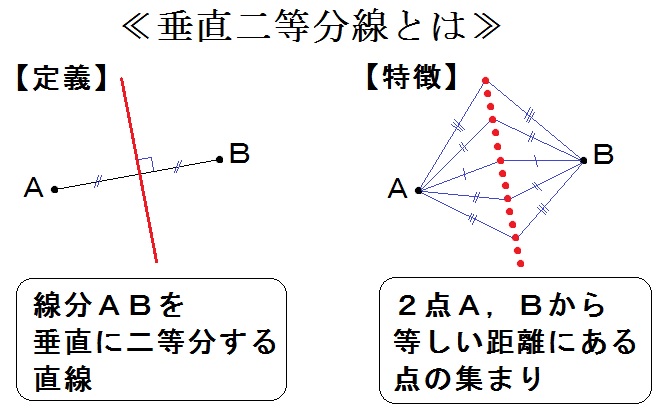



中学数学 平面図形 のコツ 垂直二等分線を使った作図
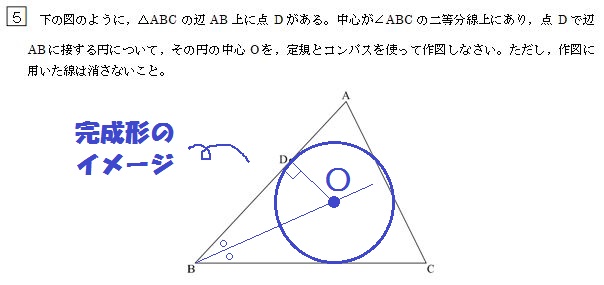



中学数学 平面図形 のコツ 角の二等分線 垂線を使った作図




基本の作図 5ステップでわかる 角の二等分線の書き方 Qikeru 学びを楽しくわかりやすく




基本 垂線二等分線の作図 なかけんの数学ノート




作図の3種類 垂直二等分線 角の二等分線 垂線 は 実は同じ図形だ 東大に文理両方で合格した男が綴る 受験の戦略




垂直二等分線 の作図方法 コンパス 定規 数学fun



Studydoctor角の二等分線の作図と利用 中学1年数学 Studydoctor



角の二等分線の書き方 学活ブログ
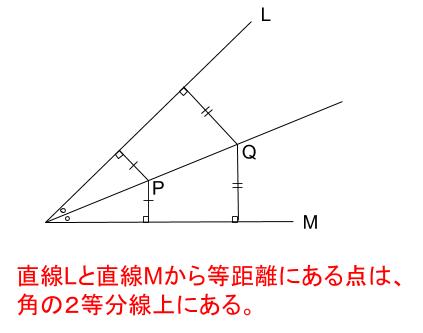



中学数学 作図 垂直二等分線 角の二等分線 中学数学の無料オンライン学習サイトchu Su
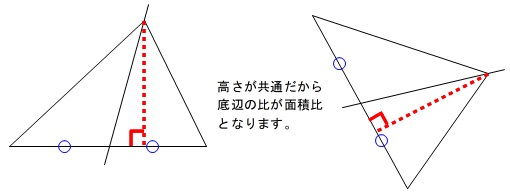



三角形の面積を直線が二等分する2つのパターン




正三角形 の作図方法 コンパス 定規 数学fun




作図 三角形の面積を 頂点を通らない直線で二等分せよ 初等幾何学 Youtube



0 件のコメント:
コメントを投稿